The probekins kins module is a trivkins module with optional Z correction. By default, probekins behaves like the trivkins module.
The purpose of probekins is to aid milling slightly warped workpiece surfaces, or deal with a machine imprecision, like for instance when milling a PCB when the board is not ideally horizontal after clamping, or slightly bent or warped. The idea is to probe the actual surface at several points covering the whole milling area, and generate Z correction values from the probed values by interpolating between neighbouring points.
Z corrections are applied when a Z correction mesh is loaded into probekins, and z correction is turned on by a HAL pin. Then the Z value of the programmed point is corrected by the Z value of the mesh at the given X/Y position.
A mesh consists of neighbouring triangles, which is normally generated automatically from a set of probed points, but could as well also be generated by hand. The probed points, or the workpiece for that matter, may be in arbitrary positions, i.e. need not be rectangular. The intended milling area should be covered by the probed points.
In G code:
(PROBEOPEN probe.txt) G38.2 X... ... (PROBECLOSE)
$ probe2stl [-i inifile] <probe.txt |stlcorr --load
To activate Z correction:
$ halcmd setp probekins.enable-z-correct 1
As long as probekins.enable-z-correct is zero, it behaves exactly like the trivkins module, and also incurs no runtime overhead.
Assume you have a mill with a 10in x 10in x/y usable area. You probe the workpiece at a few irregular points, the resulting x/y/z values are stored in a file called probe.txt and look like so:
-100 200 0.5 210 -120 0.2 -150 111 2.1 -44 -121 1.2 -12 180 1.4
To generate, and visualize the correction mesh, run:
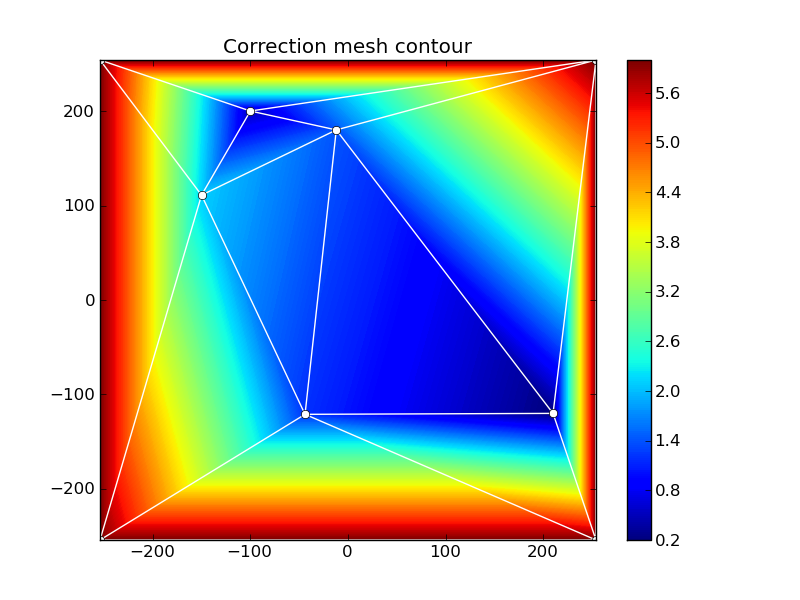
$ probe2stl <probe.txt | stlvis.py -b -254,-254,254,254
The color bar gives an indication of the Z correction applied at the given x/y value - for instance, around x=0,y=0 the correction value is roughly 1.16 (guessed from the color bar). Note that points outside the polygon (actually the convex hull) of the probed points are not Z-corrected - white means 'no Z correction':
The preview generated by stlvis looks like so: 
One way to deal with this is to add the machine boundary points to the set of 'probed' points, so they are included in the mesh. This can be done like so:
$ probe2stl -i <inifile> <probe.txt | stlvis -b -254,-254,254,254
The -i <inifile> option makes probe2stl read the AXIS_0 and AXIS_1 MIN_LIMIT and MAX_LIMIT values, and add them to the set of probed points (the TRAJ/UNITS setting is adhered - all output of stlvis and probe2stl is in mm). By default, the machine boundary points are assiged Z=0. This results in the following mesh: 
Note that 'descending to zero' at the machine boundaries might not be safest option - with the '-z value' option, you can make the correction surface 'rise' towards the machine edges:
$ probe2stl -z 6 -i <inifile> <probe.txt | stlvis -b -254,-254,254,254
The resulting correction looks like this:
Adding the machine boundaries will avoid following errors because corrections are now 'more continuous' in x/y direction.
The correction is active only with the polygon defined by the probe points and is zero outside.
To correct a bent surface of a machine, one would want to use a mesh which contains the complete work area.
One way to achieve this is to do a simple three-point probe, and scale the 'mesh' (which in fact is now a single triangle covering the whole work area) by a large factor like so:
$ stlcorr --scale 100,100,100 --load probe.stl
The arguments to the --scale flag are the scaling factor in X,Y and Z direction. To preserve angles, the X,Y an Z factors need to be identical.
stlcorr also understands --rotate deg,deg,deg and --translate xoffset,yoffset,zoffset flags.
Search the hal files for 'trivkins' and adapt like so:
# first load all the RT modules that will be needed # kinematics #loadrt trivkins loadrt probekins size=2048
The 'size=' parameter defines the shared memory segment size used for the Z correction mesh. It currently uses 8 + number of uniqe points * 24 + number of triangles * 12 bytes.
$ probe2stl -z 6 -i <inifile> <probe.txt | stlcorr --load
$ stlcorr --load <file.stl>
This will fail if the shared memory segment is too small for the correction mesh. If so, increase the size= parameter when loading the probekins module. The error message will tell how much memory is needed.
$ stlcorr --print
$ stlcorr.py --clear
To convert a probe file to a mesh:
To visualize the mesh derived from a probe file:
The probekins module and supporting files are availaible at http://git.mah.priv.at/gitweb/emc2-dev.git/shortlog/refs/heads/probekins .
Beware: this is at an early stage and not extensively tested. Feedback is welcome.
The matplotlib package is required to run stlvis. The current Ubuntu python-matplotlib package is too old (even in 10.04) for stlvis and unfortunately a recent matplotlib backport isnt currently available.
Proceed like so: Uninstall matplotlib from the package archive in case it was installed:
$ sudo apt-get remove python-matplotlib $ sudo apt-get install easy_install $ sudo easy_install matplotlib
The correction mesh is a set of triangles specified by an STL file (see http://en.wikipedia.org/wiki/STL_%28file_format%29) . It is exposed by a HAL shared memory segment, and loaded by using the hal.shm() function.
Probe2stl creates a Delauney triangulation of the probe points, and outputs an STL file.
The advantage of using a mesh of triangles over a rectangular mesh lies in the aribtrary shape and density of probe points.
If a point (x,y) lies within the one of the triangles, it's z value is adjusted by the interpolated value on the enclosing triangle. Points outside any triangle are not corrected for. This means the correction value 'falls off the cliff' at the enclosing polygon.
The triangles are tested in the order specified in the file, so there could be a 'later' larger triangle enclosing or overlapping an earlier one.
The algorithm is based on a sequential test of all triangles until first match. The line/triangle intersection test is very fast (< 1 usec/triangle on my box), nevertheless this is an O(number of triangles) implementation. There are numerous ways to optimize this, like adding a kd-tree to speed up lookup of candidate triangles.
Here's an example STL file containing two triangles:
solid
facet normal 0 1 1
outer loop
vertex 0 0 0
vertex 0 5 0
vertex 5 0 2
endloop
endfacet
facet normal 2 3 4
outer loop
vertex 1 1 1
vertex -1 -1 1
vertex 1 -1 2
endloop
endfacet
endsolid
The normal vectors ('facet normal x y z') are ignored and can be left as zero values for the purpose of describing a correction mesh.
The above works 'in principle' BUT it needs serious testing, in particular:
I have observed strange results (erratic Z correction values) with moves along mesh boundaries. I have not dug into it deeply enough, but my gut feeling is this could be a numerical accuracy issue where a point on a boundary between triangles happens to match neither triangle and thus 'falls on the floor' (getting a zero Z correction value).
I am open to suggestions how this can be detected and fixed. One obvious way would be to enlarge the triangles by some epsilon value, to assure they overlap - in case this is the actual cause. A possible test strategy would be to test the number of triangle hits.
note this error can cause serious damage to a machine!